O que é SciPy?

O projeto SciPy é uma coleção de bibliotecas Python open-source para matemática, ciência e engenharia, incluindo o NumPy e o matplotlib. Por outro lado, parte do projeto é a biblioteca scipy, que chamaremos apenas de SciPy. Ela contém como submódulos a maioria das ferramentas que se espera de um software para cientistas, incluindo funções especiais, integração, otimização, interpolação, transformadas de Fourier, processamento de sinais, álgebra linear, estatística e processamento de imagens. Veja este link.

Nosso tutorial cobre apenas algumas tarefas comuns que ilustram o uso da biblioteca e, como os anteriores, está dividido em seções para facilitar a consulta. Cada seção é um exemplo independente, e elas podem ser lidas em qualquer ordem.

Antes de tudo, importe o NumPy e o pyplot:

import numpy as np
import matplotlib.pyplot as plt

Ajustando parâmetros de curvas com curve_fit()

curve_fit() é uma função do módulo scipy.optimize. Ela recebe uma função e um conjunto de dados, e retorna os parâmetros da função que a ajustam melhor aos dados segundo o critério dos mínimos quadrados. Isto é, dada uma função , na variável com parâmetro , e um conjunto de dados experimentais , o curve_fit() encontra o parâmetro tal que a soma

é mínima. Isto também é chamado regressão.

A chamada da função curve_fit() tem a forma típica:

curve_fit(func, dadosx, dadosy, p0, errosy)

func() é a função cujos parâmetros se deseja descobrir; ela recebe a variável primeiro e os parâmetros depois: func(x, a, b, ...). dadosx e dadosy são sequências (arrays) de dados, onde x é a variável independente e y é dependente. p0 é um palpite inicial para os valores dos parâmetros, e portanto é uma lista de tamanho igual ao número de parâmetros que a função recebe (não contando a variável dependente x). errosy é uma sequência opcional que indica os erros nas medidas da variável dependente. Supõe-se que os erros em x são desprezíveis (se isto não for verdade, há métodos mais complicados que podem lidar também com erros em x).

Vejamos um caso simples. Como fazer a regressão de uma reta com o curve_fit()?

Primeiro definimos a função func que será ajustada. Ela tem dois parâmetros: o coeficiente angular a e o coeficiente linear b:

def func(x, a, b):
    return a*x + b

Agora, os dados. Vamos usar a seguinte tabela (dados.dat):

8e-3    1.403
10e-3   1.378
12e-3   1.344
13e-3   1.338
17e-3   1.280
18e-3   1.282
22e-3   1.232
29e-3   1.142

Carregando como array do numpy:

x, y = np.loadtxt('dados.dat').T

Agora usamos a função curve_fit. Ela retorna uma lista de parâmetros e uma matriz de covariância. Vamos chamar a primeira de params e a segunda de mcov:

from scipy.optimize import curve_fit
params, mcov = curve_fit(func, x, y)

Os elementos da diagonal de mcov são as variâncias de a e b, ou seja, o quadrado dos desvios-padrão, que identificamos como o erro associado aos parâmetros a e b:

a, b = params
a_err, b_err = np.sqrt(np.diag(mcov))

Vamos graficar reta ajustada e os pontos da tabela para ver o que está acontecendo:

t = np.array([0, 0.04])
plt.scatter(x, y)
plt.plot(t, func(t, a, b))

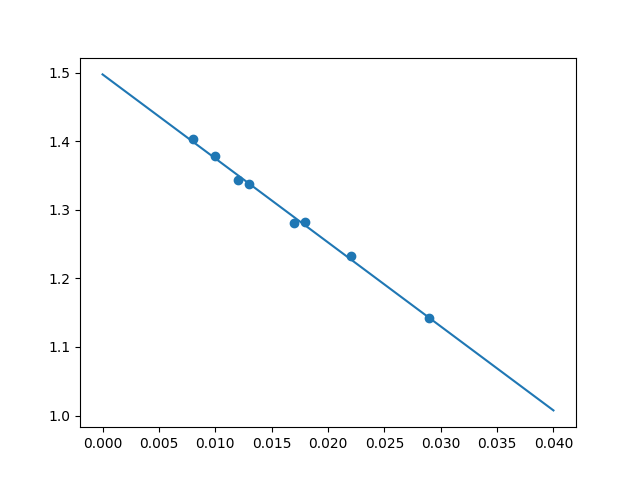
Ajuste de uma reta.

Um excelente ajuste! Se quisermos os valores dos parâmetros:

print(a, a_err)
print(b, b_err)

O que fizemos acima é absolutamente genérico e se aplica a qualquer tipo de função. Vamos a um exemplo mais complicado. A lei de Planck

dá o espectro de um corpo negro em função da frequência para uma determinada temperatura . Vamos supor que, das constantes que aparecem na equação, apenas o valor de é conhecido, mas temos estimativas das ordens de grandeza de e . Também conhecemos a temperatura do experimento. Podemos determinar as constantes de Planck e de Boltzmann com um único ajuste de curva. Por exemplo, suponha que temos os seguintes dados experimentais salvos em corponegro.dat:

# T = 300 K
# frequência, radiança espectral (unidades do SI)
0.50e13   1.02e-12
0.82e13   2.57e-12
1.14e13   4.42e-12
1.46e13   4.69e-12
1.79e13   5.35e-12
2.11e13   4.94e-12
2.43e13   4.55e-12
2.75e13   3.15e-12
3.07e13   3.22e-12
3.39e13   2.56e-12
3.71e13   1.90e-12
4.04e13   1.63e-12
4.36e13   1.02e-12
4.68e13   1.46e-12
5.00e13   0.41e-12

Então:

# Define a função (lei de Planck)
T, c = 300, 299792458
def Bnu_corpo_negro(nu, h, k):
    return 2*h*(nu**3/c**2) * (1 / (np.exp(h*nu/(k*T)) - 1))

# Carrega os dados
nu_dados, Bnu_dados = np.loadtxt('corponegro.dat').T

# Faz o ajuste com as estimativas iniciais 1e-34 e 1e-23 para h e k
params, mcov = curve_fit(Bnu_corpo_negro, nu_dados, Bnu_dados,
                         [1e-34, 1e-23])
h, k = params
h_err, k_err = np.sqrt(np.diag(mcov))

Obtivemos os parâmetros e . Compare com os valores precisos e — nada mau!. Finalmente, vamos graficar os dados e a curva ajustada:

plt.plot(nu_dados, Bnu_dados, 'o', label='Dados')
nu = np.linspace(1, 5.5e13, 100)
plt.plot(nu, Bnu_corpo_negro(nu, h, k), label='Ajuste')
plt.legend()

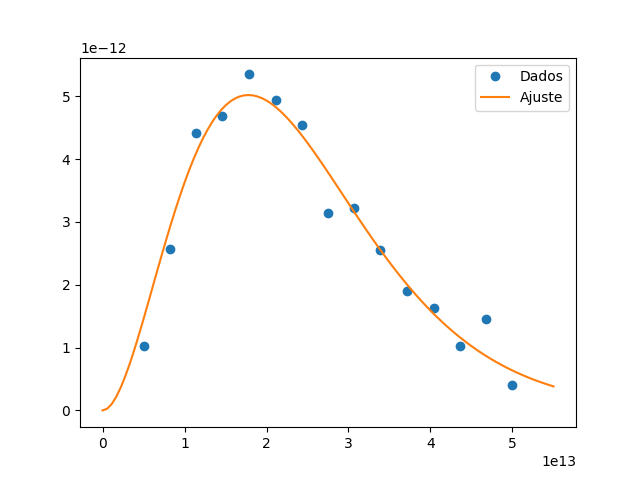
Radiação de corpo negro: curva ajustada e dados.

O curve_fit funciona por aproximações sucessivas: em cada iteração, ele modifica um pouco os parâmetros para se aproximar do mínimo. Note que, tentando fazer o ajuste com estimativas iniciais ruins (por exemplo, 0 ou 1) o curve_fit não converge e não conseguimos a solução. É sempre bom ter uma estimativa inicial ao menos na ordem de grandeza correta.

O módulo scipy.optimize também tem funções para cálculo de mínimos locais e globais e para encontrar raízes e soluções de sistemas de muitas variáveis. Consulte a documentação para saber mais.

Transformadas de Fourier com o fftpack

O pacote scipy.fftpack faz transformadas de Fourier discretas e convoluções (veja o tutorial oficial para uma discussão maior do que isto significa). Vamos ilustrar seu uso (e interpretação dos resultados) fazendo transformadas de Fourier de funções 1D.

A transformada de Fourier da função real (ou complexa) é uma função complexa da frequência . A ideia geral é decompor a função como uma combinação de diversas oscilações harmônicas da forma :

Assim o módulo de indica quão fortemente a frequência ‘‘está presente’’ no sinal , enquanto seu argumento indica a fase da onda com esta frequência. Para nosso exemplo, vamos usar um sinal simples: uma onda senoide que cai exponencialmente com o tempo (como o som de um diapasão).

Começamos importando o pacote:

from scipy import fftpack

Usando um shell interativo do Python, podemos gerar nosso sinal e exibir seu gráfico com o código

f = 5    # frequência em Hertz
fs = 100 # frequência de amostragem
T = 3    # tempo total
A = 0.1  # taxa de decaimento

t = np.linspace(0, T, T * fs + 1)
y = np.exp(-A*t) * np.cos(2*np.pi*f * t)
plt.plot(t, y)
plt.show()

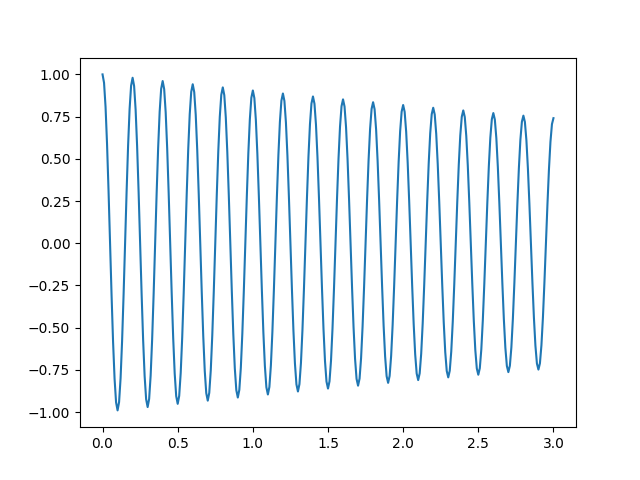
Sinal senoide decaindo com o tempo.

É importante notar que esta é uma amostra finita de pontos igualmente espaçados da nossa função matemática restrita a um intervalo, como se espera de quaisquer dados reais (por exemplo, som). Nestas condições, pode-se aplicar o algoritmo Fast Fourier Transform (FFT) para obter uma amostra também discreta, finita e igualmente espaçada da transformada . É isto que as funções do scipy.fftpack fazem.

Para calcular nossa transformada, vamos usar as funções fft e fftfreq. A primeira calcula os valores da transformada, e a segunda nos ajuda a calcular as frequências na amostra:

transf = fftpack.fft(y)
freqs = fftpack.fftfreq(len(y)) * fs

Agora (freqs, transf) nos dá o gráfico de , assim como (t, y) nos deram antes o gráfico de :

plt.plot(freqs, np.abs(transf))
plt.show()

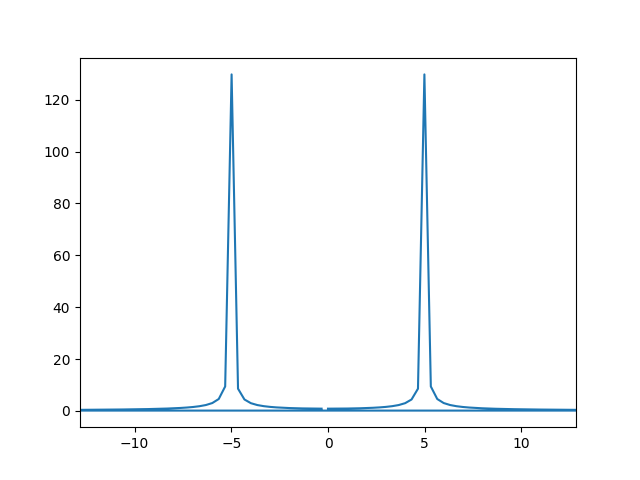
Transformada de Fourier do sinal acima.

Veja que há dois picos: um na frequência = 5 Hz, e outro em = -5 Hz. Isto era esperado, já que nosso sinal é essencialmente uma função cosseno, que se decompõe como

Mais geralmente, qualquer sinal real tem transformada de Fourier simétrica em relação à origem (o que é usado para agilizar o cálculo, por exemplo, pela função rfft). Se fizermos agora um sinal complexo, podemos ter uma transformada não-simétrica, com um único pico:

y2 = np.exp((-0.1 + 2*np.pi*f*1j)*t)
transf2 = fftpack.fft(y2)
plt.plot(freqs, np.abs(transf2))
plt.show()

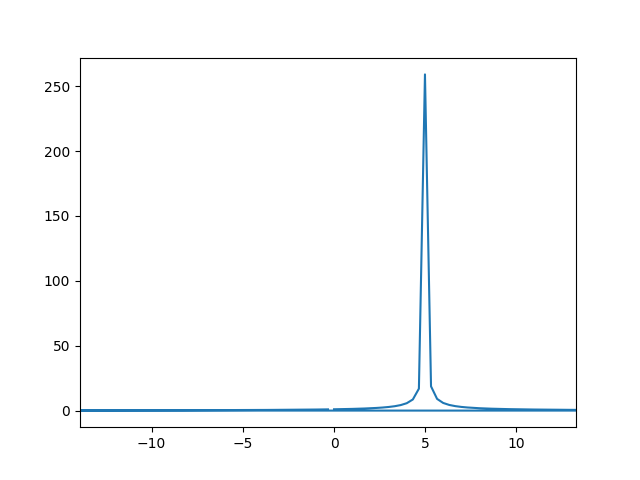
Transformada de Fourier de um sinal complexo.

Finalmente, podemos inverter a operação, fazendo uma transformada inversa de Fourier com a função ifft. Ela reconstrói totalmente o sinal original:

inv = fftpack.ifft(transf)
plt.plot(t, inv)
plt.plot(t, y)
plt.show()       # gráficos se sobrepõem

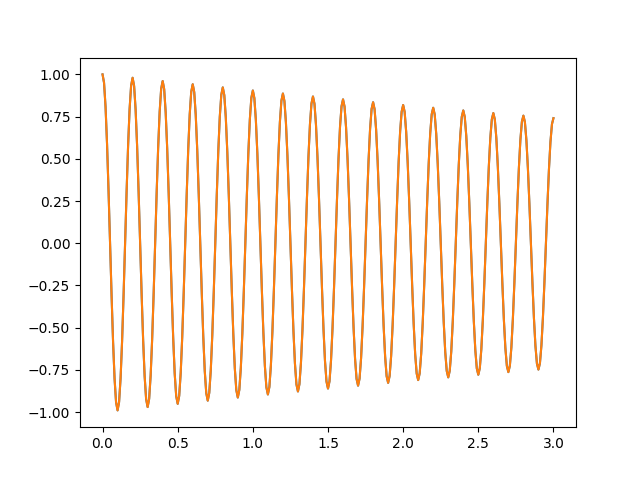
O gráfico do sinal original e do sinal reconstruído pela transformada inversa de Fourier.

Para saber como fazer transformadas em dimensões, convoluções e outras coisas, consulte a documentação.

Calculando integrais com integrate

O módulo scipy.integrate contém funções para cálculo de integrais (em qualquer número de dimensões) e solução de sistemas equações diferenciais ordinárias. Vamos exemplificar o uso de algumas delas.

O cálculo de uma integral definida também é conhecido como quadratura, e por isso o integrate fornece as funções quad para cálculo de integrais em uma dimensão, dblquad para integrais duplas, tplquad para triplas e nquad para integrais de dimensão qualquer. Essas funções são para uso genérico, fornecendo como resultado uma aproximação da integral e uma estimativa (cota superior) do erro.

Como exemplo, vamos calcular uma integral da função com quad.

from scipy import integrate

# Exemplo: função sinc ('seno cardinal')
@np.vectorize
def f(x):
    if x == 0:
        return 1
    return np.sin(x) / x

# Intervalo de integração
a, b = -6*np.pi, 6*np.pi

# Mostrando a curva
x = np.linspace(a, b, 300)
y = f(x)
plt.fill_between(x, y)
plt.show()

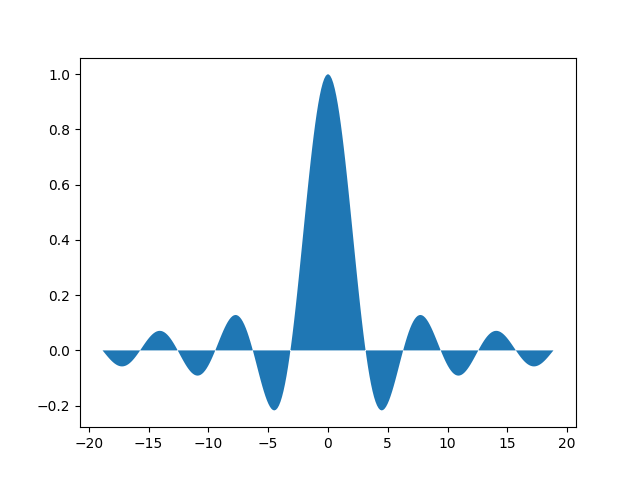
Área integrada da função sinc entre -6π e 6π.

O cálculo em si é feito em uma linha, dando como parâmetros à função quad nossa o integrando f e os limites de integração:

resultado = integrate.quad(f, a, b)
print(resultado)  # Retorna valor e estimativa de erro

Isto dá o resultado com 12 dígitos de precisão. Se mais precisão for desejada, isto pode ser especificado com o parâmetro epsabs (tolerância absoluta de erro). Veja a documentação.

Para limites de integração infinitos, usamos o objeto np.inf. Por exemplo, podemos calcular

com o código

def g(x):
    return np.exp(-x*x)
res, err = integrate.quad(g, 0, np.inf)
print(res, np.sqrt(np.pi)/2) # compara com resultado analítico

e analogamente usa-se -np.inf para .

O integrate também pode fazer cálculos com sistemas de equações diferenciais ordinárias (EDOs). O problema mais comum é o problema de valor inicial (PVI) – dados valores das variáveis em , encontrar sua evolução temporal para . A função odeint se encarrega diretamente disto, resolvendo PVIs para sistemas de EDOs de ordem 1 (isto é, em que se especifica as primeiras derivadas de cada variável em termos de todas as variáveis, mas sem envolver derivadas de ordem superior).

Isto parece, mas não é uma restrição: na verdade, todos os sistemas de EDOs podem ser reduzidos a sistemas de ordem 1 se transformarmos algumas derivadas em variáveis (aumentando a quantidade de equações). Por exemplo, a equação do oscilador harmônico

é de segunda ordem, mas pode ser transformada num sistema de equações de primeira ordem:

o truque é exatamente tomar a velocidade como uma nova variável . Isto sempre pode ser feito para reduzir um sistema de qualquer ordem a um sistema de ordem 1.

Vamos aproveitar o exemplo e integrar o oscilador harmônico com as condições iniciais , . Primeiro definimos o sistema de equações acima (que é um campo vetorial no plano xy) pela função campo1:

def campo1(ponto, t):
    x, y = ponto
    return [y, -x]  # derivadas temporarais de x e y

Agora definimos o intervalo de integração t (um array do numpy) e as condições iniciais (uma lista de números):

t = np.linspace(0, 10, 200)  # integrar de t=0 até t=10
iniciais = [3, 0]            # x(0) e y(0)

Finalmente, passamos tudo para a função odeint, que retorna um array contendo as funções horárias e :

x, y = integrate.odeint(campo1, [3, 0], t).T

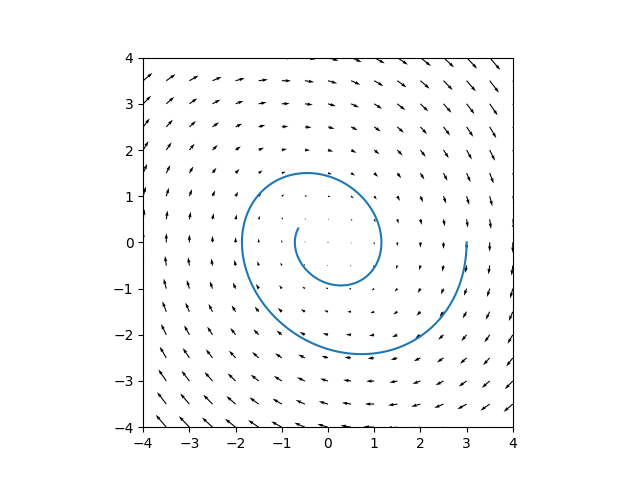
Finalmente, podemos graficar o resultado, tanto em função do tempo como apenas como uma trajetória no plano xy (conhecido em física como espaço de fase), que é uma curva integral do campo campo1:

# Plot do campo e da trajetória no espaço de fase
ax = plt.gca()
X, Y = np.meshgrid(np.arange(-5, 5, .5),
                   np.arange(-5, 5, .5))
U, V = campo1([X, Y], 0)
ax.quiver(X, Y, U, V)
ax.plot(x, y)
ax.set_aspect('equal')
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
plt.show()

# Plot dos valores de x e y em função do tempo
plt.plot(t, x, label='x')
plt.plot(t, y, label='y')
plt.legend()
plt.show()

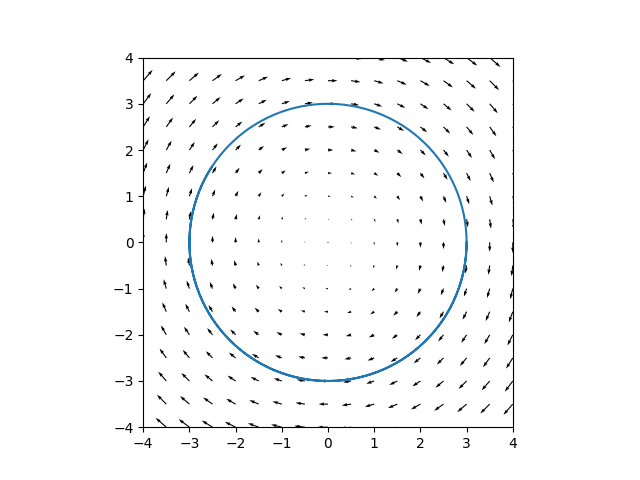
Trajetória do oscilador harmônico no espaço de fase.

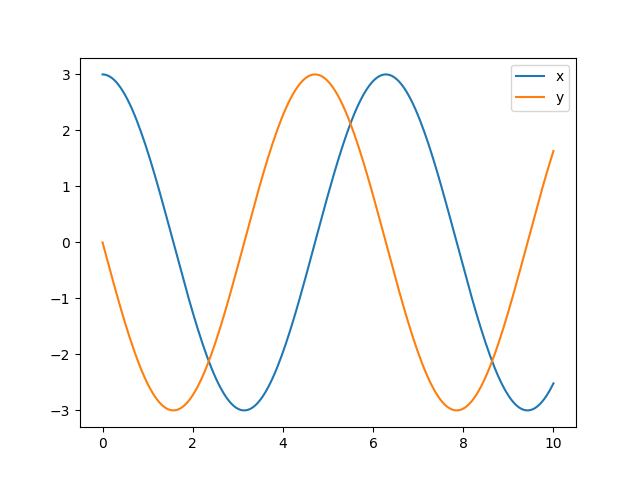
Evolução temporal das variáveis x e y.

Analogamente, poderíamos resolver a equação do oscilador amortecido

com a função de derivadas (agora dependente do parâmetro a)

def campo2(ponto, t, a):
    x, y = ponto
    return [y, -x - a*y]

A solução, desta vez, seria obtida passando-se para odeint a função campo2, o intervalo de integração, os valores de e em e também o valor do parâmetro , dado pelo parâmetro args. Se decidirmos usar as mesmas condições iniciais e :

x, y = integrate.odeint(campo2, [3, 0], t, args=(0.3,)).T

Dando o resultado

Trajetória do oscilador harmônico amortecido no espaço de fase.

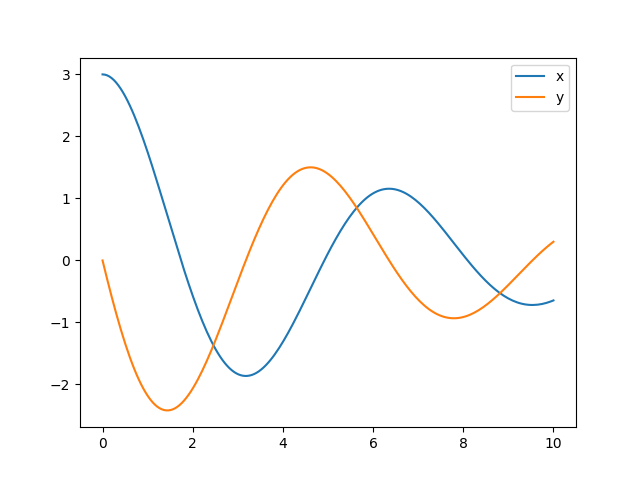
Evolução temporal das variáveis x e y para o caso amortecido.

Para informações mais detalhadas (e resolver problemas mais específicos que PVIs com intervalos de integração fixos), veja a documentação do integrate.

Licença

Este trabalho está licenciado sob a Licença Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional (BY-NC-SA 4.0 internacional) Creative Commons. Para visualizar uma cópia desta licença, visite http://creativecommons.org/licenses/by-nc-sa/4.0/.