Oscilações em membranas: Solução numérica

Solução numérica para ondas estacionárias em membranas

Introdução

Nem sempre é necessário ou possível obter a solução exata de um determinado sistema, para esses problemas usamos modelagem e simulações para obter soluções numéricas.

A ideia com essa modelagem é mostrar que apesar do problema exato ser complexo, a solução numérica é simples e têm diversas aplicações.

Equação de onda:

$\nabla^2 u = \frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}$ $\rho\frac{\partial^2 u}{\partial t^2} - \sigma\nabla^2 u = 0$

Como é feita a discretização para a equação de onda

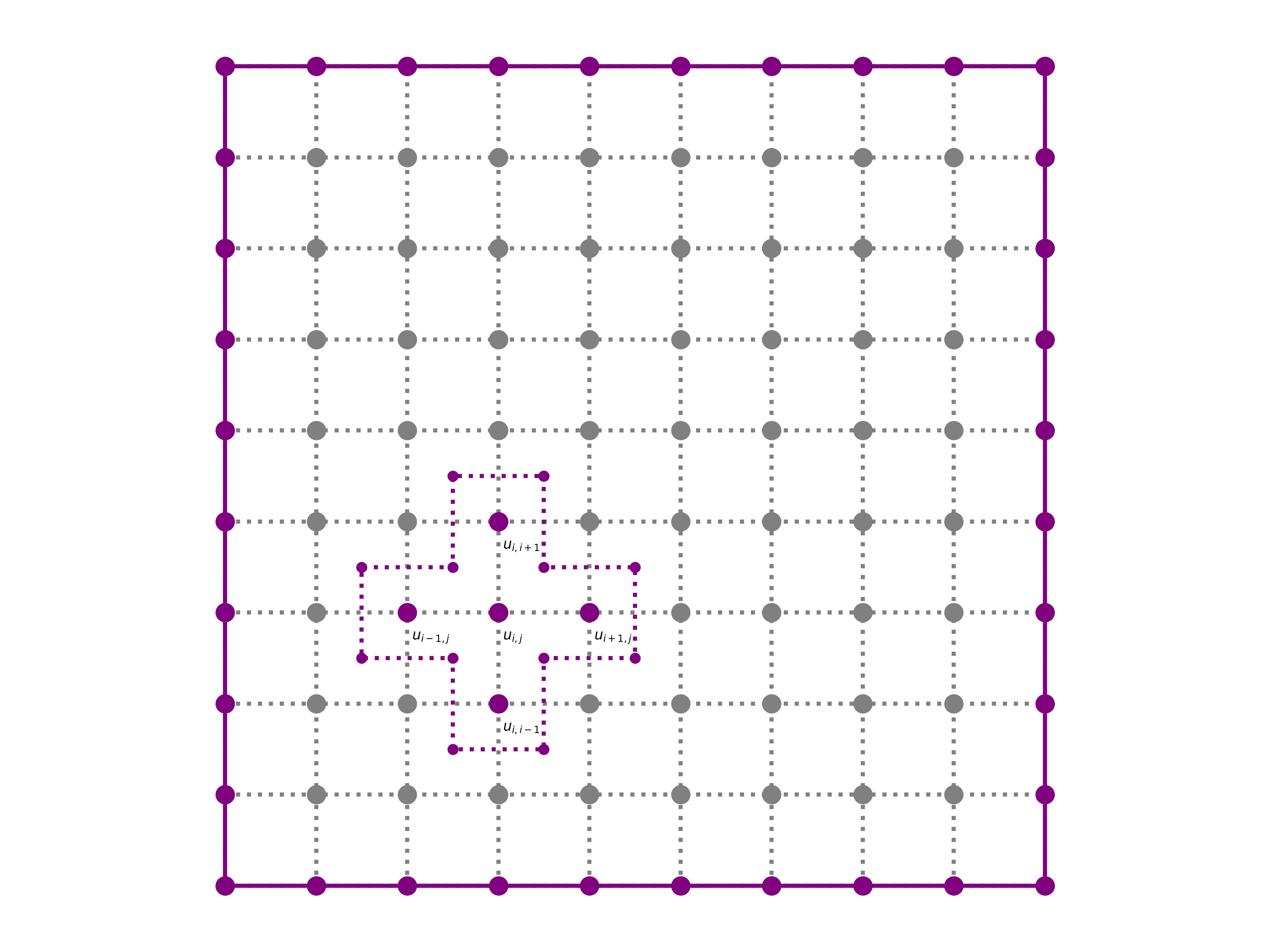
Malha de discretizando da membranda

Para a forma matricial usaremos $K = -\sigma\nabla^2$ para a modelagem:

$MU''+KU = 0$ $U(t) = \Phi\sin{(\omega t)}$ $U''(t) = -\Phi\omega^2\sin{(\omega t)}$ $K\Phi - \omega^{2}M\Phi = 0$ $K\Phi = \omega^{2}M\Phi$ $\rho\frac{d^{2}u_{ij}}{dt^{2}} - \sigma\frac{u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1}-4u_{ij}}{\delta^{2}} = 0$

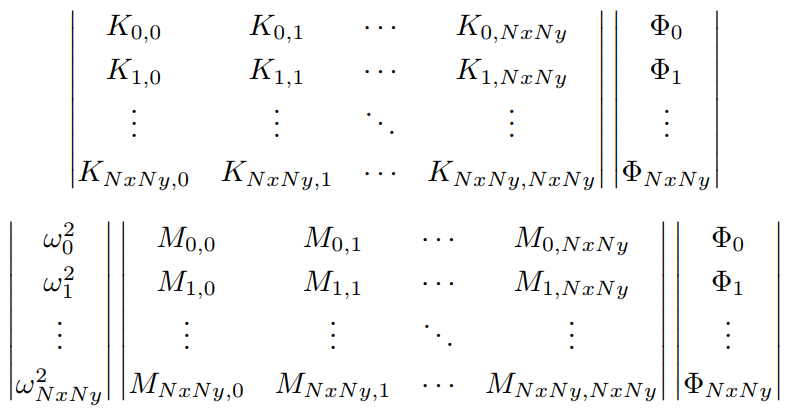
forma matricial da equação

Bibliotecas usadas

import numpy as np
import scipy.linalg as la
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d

Cria o índice global

O índice global será o que dará a forma da base do sistema. A escolha para ser desse jeito é por pura conveniência, já que o método reshape do numpy “desfaz” essa forma de indexar.

def ij2n(i,j,Nx):
    return(i + j*Nx)

Construção das matrizes K e M

Na construção das matrizes K e M irei considerar rho e sigma constantes, mas poderia passar uma função com poucas modificações

def buildKM(Nx, Ny, rho, sigma, delta, mask):
    NxNy = Nx*Ny
    K = np.zeros( (NxNy,NxNy) )
    M = np.zeros( (NxNy,NxNy) )

    for i in range(1, Nx-1):
        for j in range(1, Ny-1):
            Ic = ij2n(i,   j,   Nx)
            K[Ic,Ic] = -4

            Ie = ij2n(i+1, j,   Nx)
            K[Ic,Ie] = 1

            Iw = ij2n(i-1, j,   Nx)
            K[Ic,Iw] = 1

            In = ij2n(i,   j+1, Nx)
            K[Ic,In] = 1

            Is = ij2n(i,   j-1, Nx)
            K[Ic,Is] = 1

    K *= -sigma/(delta**2)

    for i in range(Nx):
        for j in range(Ny):
            Ic=ij2n(i, j, Nx)

            if not mask[i, j]:
                K[Ic,:]=0.
                K[:,Ic]=0.
                K[Ic,Ic]=1e9

            M[Ic,Ic] = rho

    return(K, M)

Montagem da máscara da membrana

A máscara é uma matriz com zeros e uns para facilitar na construção da forma da membrana, onde os uns são posições onde a membrana tem liberdade para mudar de posição e os zeros posições que serão travadas

def mask(Nx, Ny):
    Mk = np.ones( (Nx,Ny), np.int )

    # Define um raio que tem 40% do menor lado da malha
    r = np.floor(0.4*min(Nx, Ny))

    for i in range(Nx):
        x = i - Nx//2
        for j in range(Ny):
            y = j - Ny//2

            # Pode colocar a função que desejar no if
            if x**2 + y**2 > r**2:
                # Define com 0 os pontos da membrana que estão travados
                Mk[i,j] = 0

    # Trava as bordas
    Mk[ 0, :] = 0
    Mk[-1, :] = 0
    Mk[ :, 0] = 0
    Mk[ :,-1] = 0

    return Mk

Como resolver o sistema e obter os Autovalores e Autovetores

Funcionamento da função de eig do scipy

a = matriz (n x n)
b = matriz (n x n)
D = autovalores (n)
V = autovetores (n x n)

[D, V] = scipy.linalg.eig(a, b)
a*V = D*b*V

$aV = DbV$ $K\Phi = \omega^{2}M\Phi$

def solve(K, M):
    omega2, phi = la.eig(K, M)

    # Ordena os resultados
    idx = np.argsort(omega2)
    omega2 = omega2[idx]
    phi = phi[:,idx]
    omega = np.sqrt(omega2)

    return(phi.real, omega.real)

Atribuindo valores

Nx = int(input("Nx: "))
Ny = int(input("Ny: "))
sigma = float(input("sigma: "))
rho = float(input("rho: "))
Lx = 1.
delta = Lx/(Nx-1)

K, M = buildKM(Nx, Ny, rho, sigma, delta, mask(Nx, Ny))

phi, omega = solve(K, M)

Visualização dos dados

while True:
    k = int(input("Digite o indice do modo: "))
    ciclos = float(input("Digite o número de ciclos: "))
    Z = phi[:, k].reshape(Nx, Ny)

    dt = (ciclos*2*np.pi)/omega[k]

    zlim = np.max(np.abs(Z))*1.02

    x = range(Nx)
    y = range(Ny)

    X, Y = np.meshgrid(x, y)

    fig = plt.figure(dpi=200)
    ax = plt.axes(projection='3d')

    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    ax.set_xlim(0, Nx-1)
    ax.set_ylim(0, Ny-1)
    ax.set_zlim(-zlim, zlim)
    plt.tight_layout()
    plt.ion()

    for i in np.linspace(0, dt, 20):
        ax.clear()
        ax.set_zlim(-zlim, zlim)
        ax.plot_surface(X, Y, Z*np.sin(omega[k]*i), cmap="binary")
        plt.show()
        plt.pause(0.001)